Nth-Iteration

Jorrit just won the best paper award at Intetain; pretty awesome!

I am happy to announce that Lianne Ippel her paper (in joint work with Maurits Kaptein & Jeroen Vermunt) called “Estimating Random-Intercept Models on Data Streams” is accepted for publication in Computational Statistics and Data Analysis (CSDA). This is awesome!

You can find an author copy of the paper here.

Cheers!

Hi,

I am happy to share that Prof. Davide Iannuzzi will be presenting some of the joint work that Robin van Emden, me (Maurits Kaptein) and Davide have been doing together at APEC-SSS 2016. The abstract can be downloaded here.

Cheers,

Maurits (by the way, currently I am at the ISBA conference which is great!)

Hi All,

A few updates: First, things are going extremely smoothly at JADS where we are setting up a new Data Science research institute. We are happy to be a part of it, and to be collaborating with some great minds (such as Prof. Dr. Eric Postma). Also, we will be sharing new work on StreamingBandit during the Social Sciences and the Internet Conference (check here, and here is an abstract of the talk). Finally, we will be presenting a poster at the ISBA 2016 conference. Check out the poster here.

We also have some cool recent work that I would like to share. First, Robin van Emden did a pretty cool visualization of how Lock in Feedback (LiFt) works in two dimensions; (not that LiFt is implemented as a policy in StreamingBandit). Check this out:

LiFT animation I from Robin van Emden on Vimeo.

 

We think its pretty cool!

Also, up and coming, some really cool work by Shuai on distributing media expenditure over different channels, and some really cool stuff by Jules implementing a) simulation functionality into StreamingBandit, and b) creating an offline evaluation methods for continuum bandit problems.

Cheers.

Hi all,

Just a brief update: A paper written by Jorrit Siebelink, Peter van den Putten, and Maurits Kaptein was recently accepted at INTETAIN 2016 which is coming up soon. Grab an author copy here.

Furthermore, we are doing some very cool project with 2 Finish companies on (1) optimizing media spending dynamically – together with Prof. Dr. Petri Parvinen – and (2) optimizing rebate offers. Both are exciting, and both use the StreamingBandit back-end. We will share results as they come available. We here also have some awesome work by a new student contributing: Shuai Yuan.

Finally, we would like to alert to JADS, the new and exciting joint data science initiative by the TU/e Eindhoven and UvT Tilburg. Maurits will be one of the staff member of JADS in years to come.

Guess that’s it for now; hope to have more updates on papers and recent work in the coming weeks.

Hi All,

Finally, our book is out!

And, I (Maurits), just yesterday gave the closing keynote for the workshop on Personalization (see here). It was a great session. My slides are available here.

Currently Persuasive 2016 is on its way, and, thanks to the organizers, its a great event! Check out the program here.

Finally, note that the publication page was updated. Check it here.

Hey,

A little technical update today. We have been playing with Bayes optimal allocation in the case of a 2-arm Bernoulli Bandit problem with finite (and rather small) horizon. The idea is to start comparing some currently popular solutions  (e.g., Thompson sampling, Gittins Index, etc.) to Bayes optimal allocation (yes, some of this has been done before…).

So, we started out implementing induction the algorithm described here in [R]. You can find the source file here. The use is straightforward:

source("bb.R")

# Arm priors:
arm1 <- c(1,1)
arm2 <- c(120,100)

# Number of remaining pulls:
n <- 5

# Compute the Delta between the arms:
res <- DeltaArm(n, arm1, arm2) 

# Print result, and which arm to play 
print(res) 
print(ifelse(res>0,"Arm1","Arm2"))

Which prints that Arm 1 should be preferred in this case (note that this is not the case when $n < 3$; for these values the exploration does not pay off since there are too little future opportunities to use the learned knowledge).

However, the implementation in bb.R ends up being a bit slow, so, using the Rcpp package, we implemented the same thing in C++. This can be called like this:

# Use the Cpp version
library(Rcpp)

# Load the compiled Cpp function:
dyn.load('BB.so')

# Arm priors:
arm1 <- c(1,1)
arm2 <- c(120,100)

# Number of remaining pulls:
n <- 5

# Compute the Delta between the arms:
res <- .Call('DeltaArm', arm1[1],arm1[2],arm2[1],arm2[2],n) 

# Print result, and which arm to play 
print(res) 
print(ifelse(res>0,"Arm1","Arm2"))

Which gives the exact same (well, with some different rounding) results but much faster.

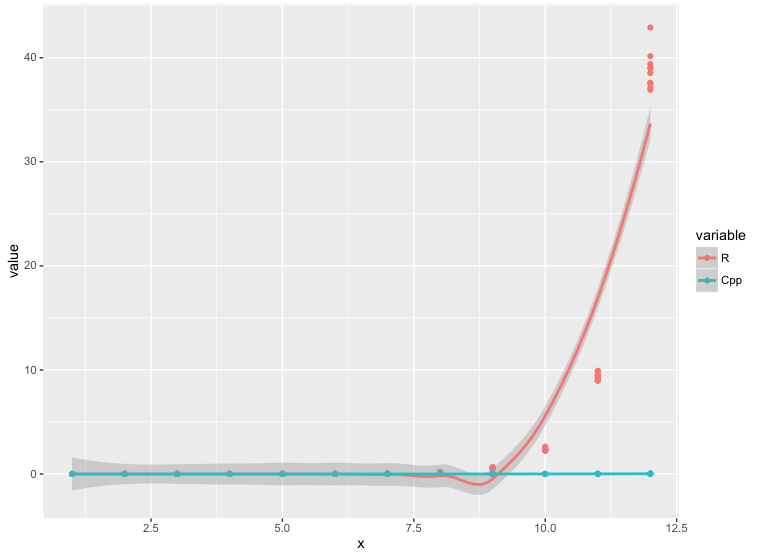
How much faster is easily seen if when doing several runs ($m=10$ in this case), for different values of the horizon $n = 1, \dots, 12$. The figure below shows the time progression of the R version and the C++ version; quite a shocking difference really. The C++ version can be downloaded in our downloads section (both the source, as well as the compiled version).

Have a great weekend!

Hi All,

Last Friday I gave a talk at IvIR, and it was awesome (thanks to Professor Helberger). We had some great discussions, and I learned a lot about the legal discussion regarding privacy and personalization. Please find my slides here.

Also, today we heard that we can present the work on StreamingBandit during Persuasive2016. Jules Kruijswijk and Maurits Kaptein will present a poster (see a short description here) during the conference. We also submitted a longer version of this description for archival on arXiv. Find the .pdf here. The arXiv link should be available tomorrow.

Let us know if you have any questions!

Hi all,

Sorry, no updates yet on StreamingBandit or our decoy effect studies; both of them are still work in progress. However, I decided to share some of the lecture notes of courses that I have been giving over the years; they might be useful for people. Also, they might contain errors: if you spot those please do let me know!

• AI at a Webscale. Course on the use of AI / ML methods and techniques for web applications at the Radboud University. See lecture notes here. The course only ran for one year (since I moved institutions afterwards), and hence the lecture notes are still pretty rough. However, they can serve as a nice outline for future courses.
• Analysis and Construction of Questionnaires. An older course that a gave in 2012,2013,2014 on questionnaire construction. Find the lecture notes here.

Tomorrow I will be giving a talk on Personalization and Persuasion at IViR Amsterdam.

Cheers,

Maurits

Hi all,

Just a few brief updates (more coming up in a few weeks when we launch a new version of StreamingBandit, launch a super cool study on decoy effects, hopefully can update you on Persuasive 2016, and the new book will be out):

1. I (Maurits) will be starting as an assistant professor of Statistics and Research Methods at the University of Tilburg from the 1st of February onwards. I will be joining the Data Science program (which is organized in collaboration with the Technical University of Eindhoven).
2. Dean Eckles and I are cranking away on a submission to KDD; we our doing a large offline evaluation of BTS. We will be sharing the code soon.

I guess that’s it for now 😉

Cheers.

ps. Well, I do want to recommend everyone to read Jaynes.